格简介(Lattice)

给定一组线性无关的基向量 (basis)

，这些基向量的线性组合 (linear combinations) 为：

而这些线性组合所组成的集合，称作这组基向量所张成的空间 (span)，也被称作向量空间。

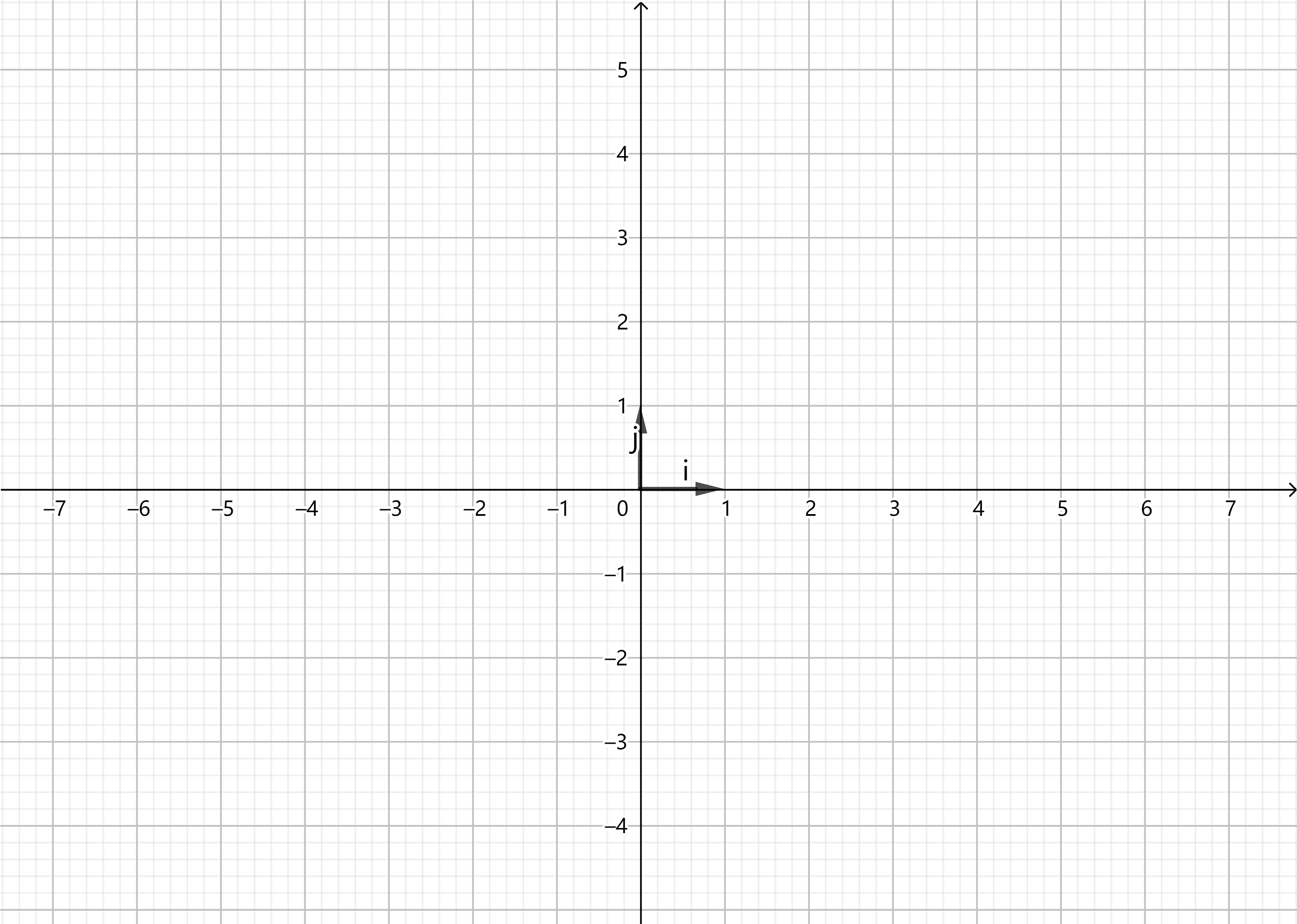
例如我们在二维平面中选取两个单位正交向量作为基向量：

那么由这两组基向量组成的所有可能的线性组合为： 其中

，其所张成的空间便是整个二维平面。

二维平面 二维平面

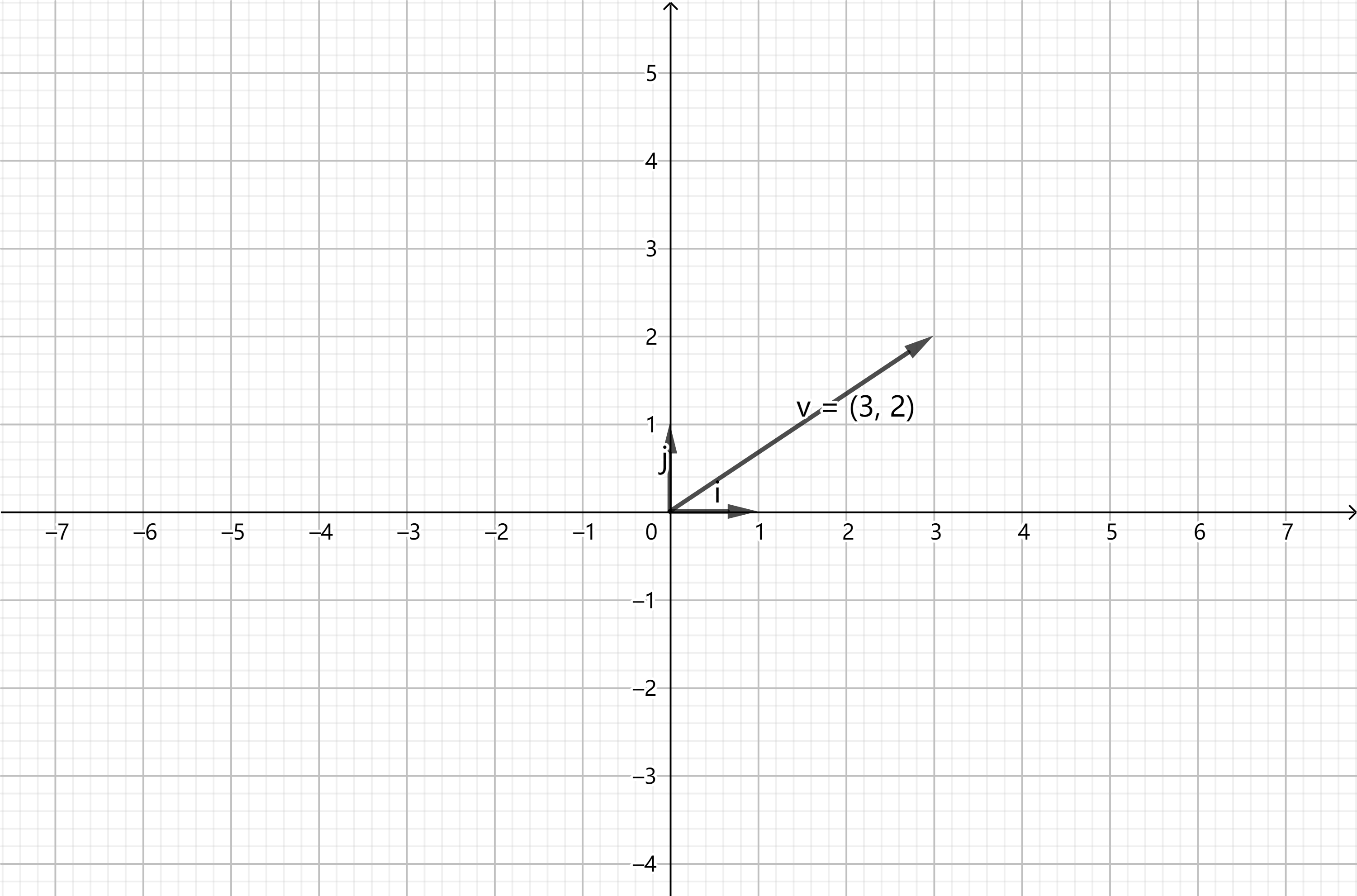
反过来，在这个二维平面上的任意一点都可以由这两个基向量的一个线性组合表示：

二维平面上一个线性组合 二维平面上一个线性组合

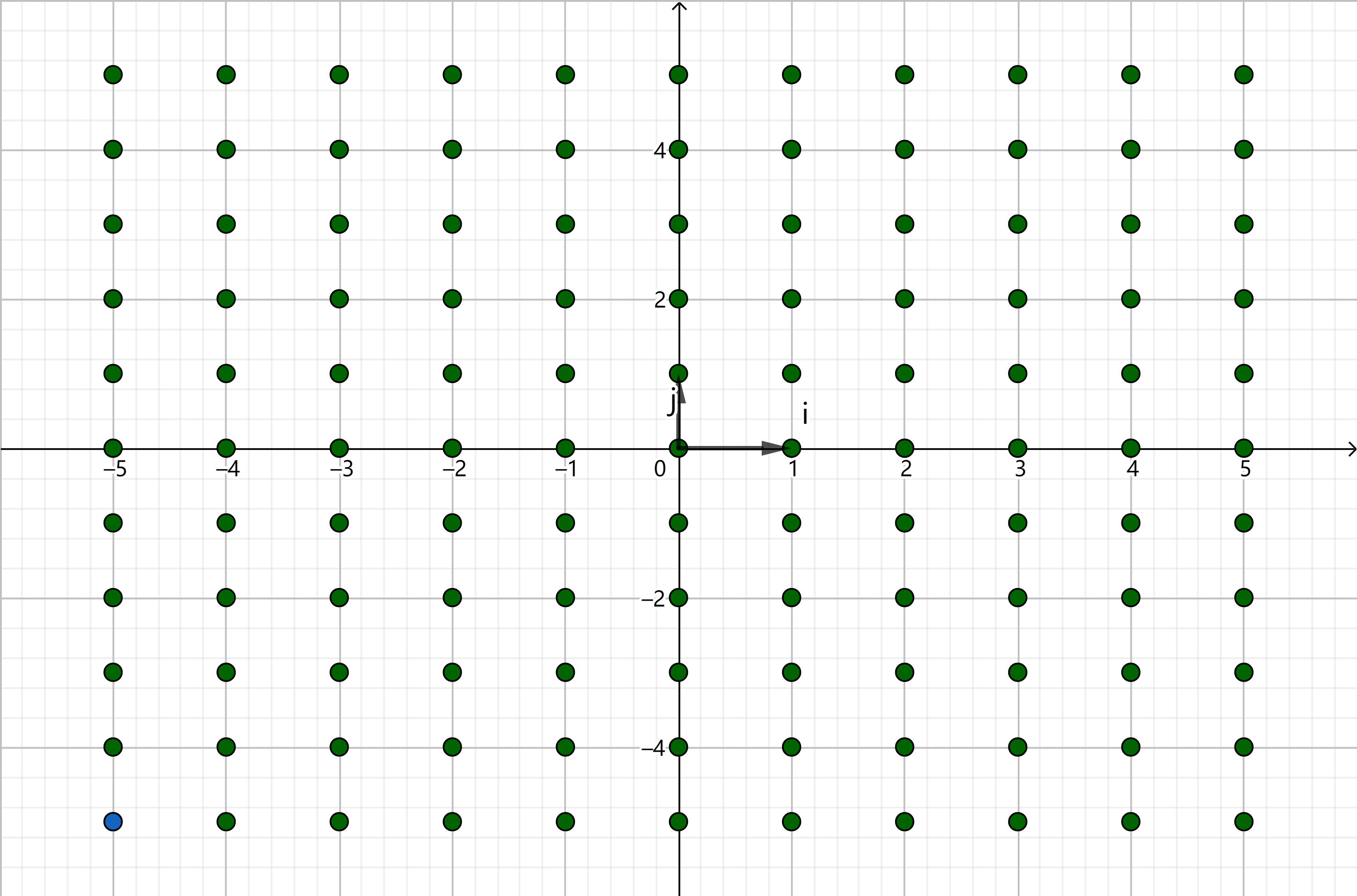
而格，就是这些基向量的所有整系数的线性组合：

这些线性组合所形成的集合就叫做这组基向量所张成的格 (lattice)，可以简单理解为离散的向量空间。

当系数不是实数而是任意整数的时候，其所张成的线性空间从无数个连续的点变成了无数个离散的点。

正交基向量张成的格 正交基向量张成的格

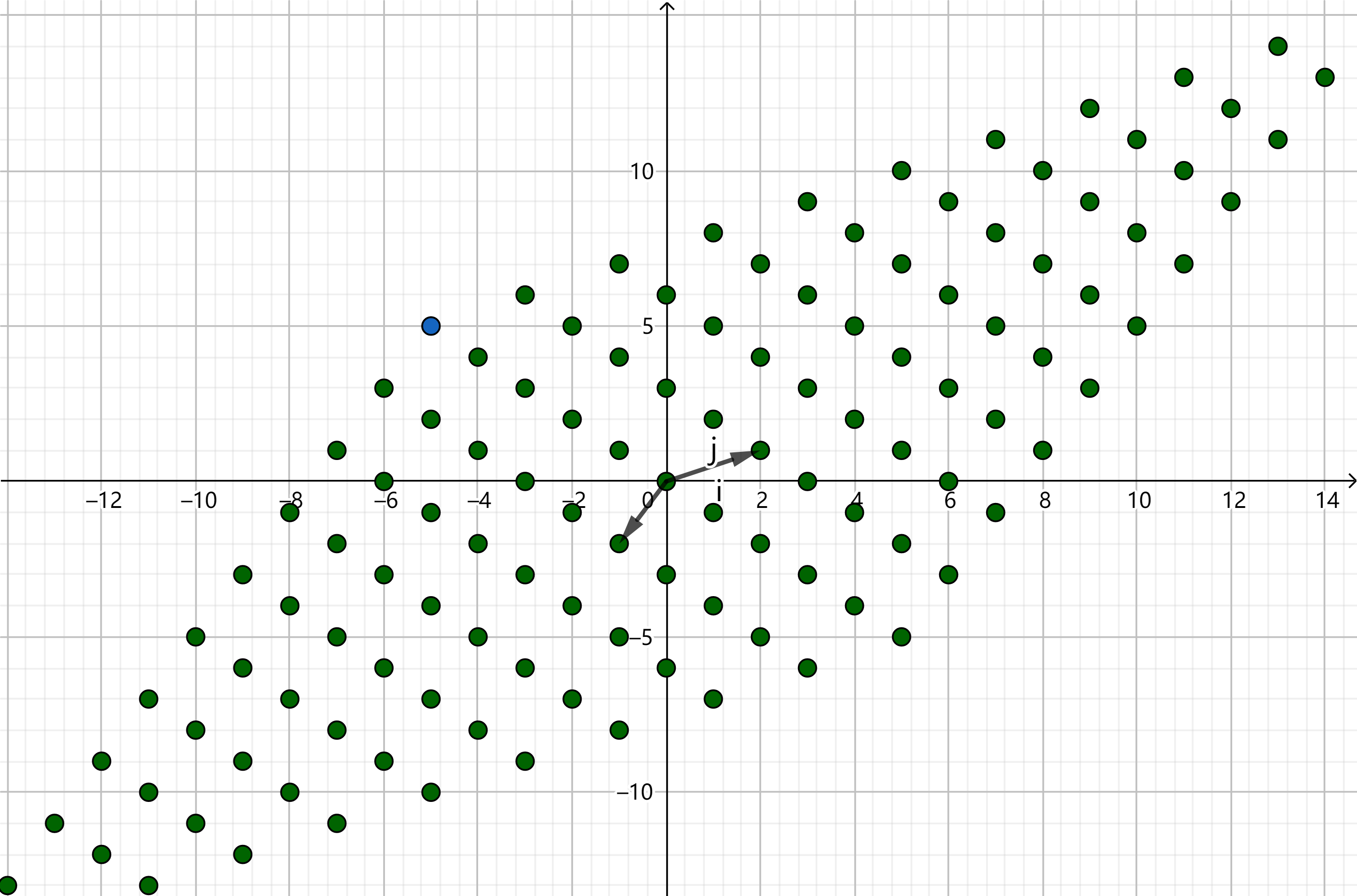
当基向量发生改变时，其所张成的格也会发生改变：

不同基向量张成的格 不同基向量张成的格

如果对原基底进行整系数线性变换，得到的新基底所张成的格仍旧不变：

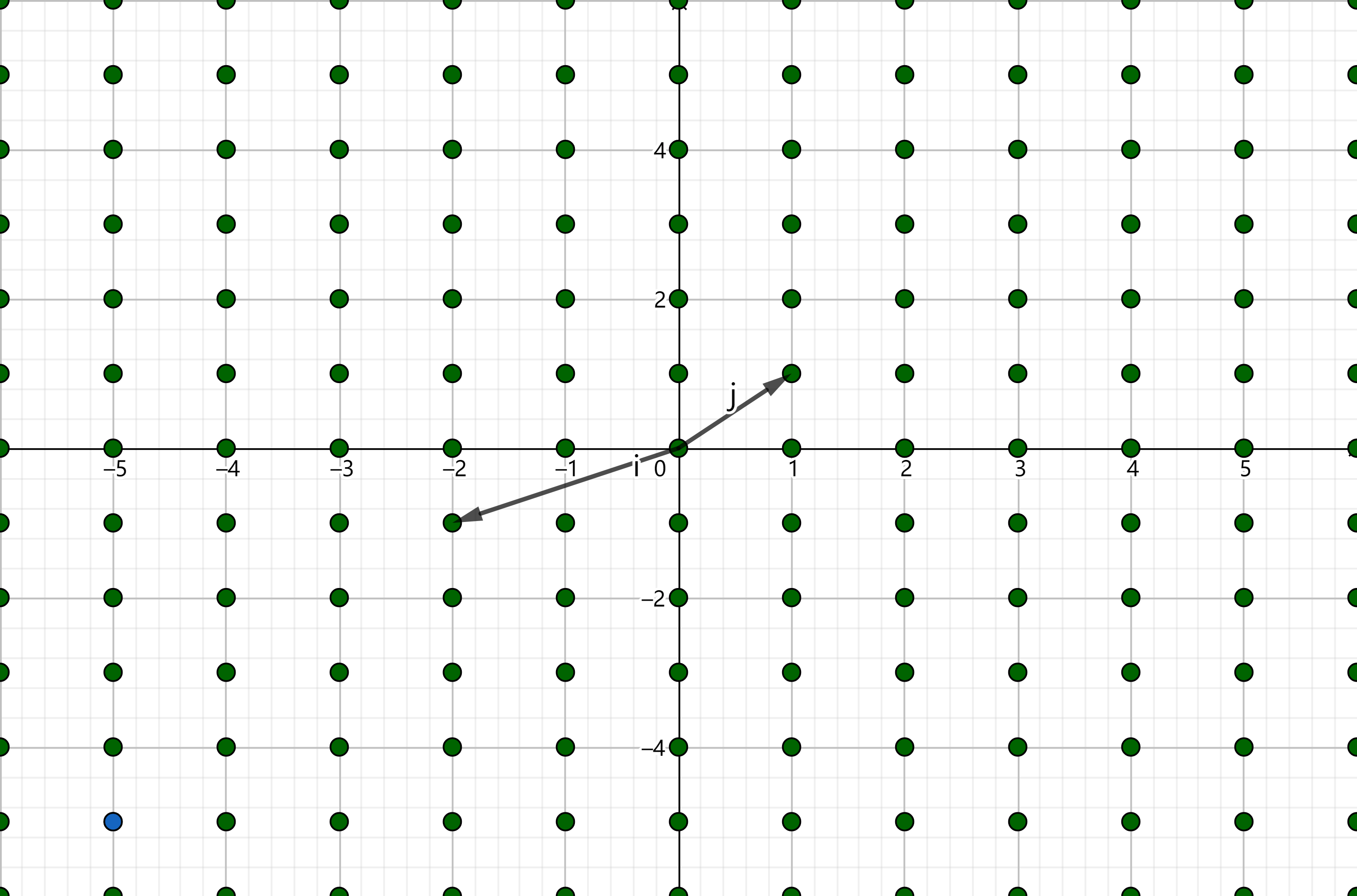相同的格 相同的格

所以我们可以发现，就算是同一个格，也可以有很多组基底。

而在格学说里，有两个知名难题：

  • SVP (最短向量问题，Shortest Vector Problem)：给定lattice和基向量，找到lattice中的一个长度最短的非零向量。
  • CVP (最近向量问题，Closest Vector Problem)：给定lattice和基向量，以及一个不在lattice上的目标向量，找到lattice中一个距离目标向量最近的格向量。

在广义上这两大难题被证明是 NP-hard 问题。

小格可以使用 Sagemath 的 LLL 算法求解格规约，但大格可能 Sagemath 提供的算法效率不够，这个时候可以借助 flatter 库进行格规约计算。

1
2
3
4
5
6
7
8
M = matrix(ZZ, [(66586820,65354729),(6513996,6393464)])
def flatter(M):
    from subprocess import check_output
    import re
    inputM = "[[" + "]\n[".join(" ".join(map(str, row)) for row in M) + "]]"
    outputM = check_output(["flatter"], input=inputM.encode())
    return matrix(M.nrows(), M.ncols(), map(int, findall(b"-?\\d+", outputM)))
flatter(M)